A reentry simulation with lift and drag forces. Uses LiftingReentry3D.m

The vehicle starts at 380 km, the ISS altitude. It does a delta-v to do a Hohmann transfer to 40 km where drag causes reentry. You can control reentry using angle of attack (d.alpha). ------------------------------------------------------------------------ See also Plot2D, TimeLabl, Dot, Mag, RK4, Unit, DVHoh, RHSLiftingReentry3D ------------------------------------------------------------------------

Contents

%-------------------------------------------------------------------------------
%    Copyright (c) 2009 Princeton Satellite Systems, Inc.
%    All Rights Reserved.
%-------------------------------------------------------------------------------

nSim           = 4800;
dT             = 1;


d.rPlanet      = 6378.165;
d.omega        = 2*pi/86400;
d.alpha        = 0;
d.l            = 10;
d.sRef         = 20;
d.oswaldEff    = 0.95;
d.aspectRatio  = 6;
d.thickness    = 0.01;
d.cLAlpha      = 10;
d.mu           = 3.9860036e5; % km/s^2
d.mass         = 100;
d.mHyper       = 7;

r0             = d.rPlanet + 380;
r              = [r0;0;0];
rI             = d.rPlanet +  40;

Hohmann transfer to 70 km

%--------------------------
[dV, dV1, dVI] = DVHoh( rI, r0, sqrt(d.mu/rI) );
v              = [0;sqrt(d.mu/r0) - dVI;0];
x0             = [r;v]; % Last number is mass of fuel

Run the sim

% Store plot points in x
%-----------------------
x = [x0 zeros(length(x0),nSim)];
f = [LiftAndDragSeaLevelToOrbit(x0,d)/d.mass zeros(3,nSim)];

for k = 1:nSim
  x(:,k+1) = RK4( @RHSLiftingReentry3D, x(:,k), dT, 0, d );
  f(:,k+1) = LiftAndDragSeaLevelToOrbit(x(:,k),d)/d.mass;
  if( Mag(x(1:3,k+1)) - d.rPlanet <= eps ) break; end

end

x    = x(:,1:(k+1));
f    = f(:,1:(k+1));

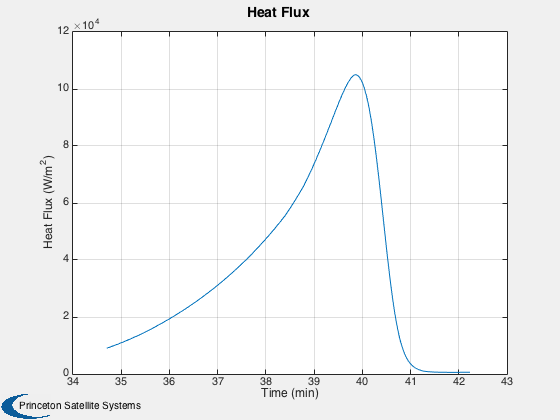
Calculate the heating rate history

%------------------------------------
d.time = (0:k)*dT;
d.velocity = Mag(x(4:6,:))*1000;
d.aoa = d.alpha;
d.altitude = (Mag(x(1:3,:)) - d.rPlanet)*1000;
k2 = find(d.altitude < 80000,1);
d.time = d.time(k2:end);
d.velocity = d.velocity(k2:end);
d.altitude = d.altitude (k2:end);
qDot = AeroHeatFlux( d, d.l, 'laminar plate' );

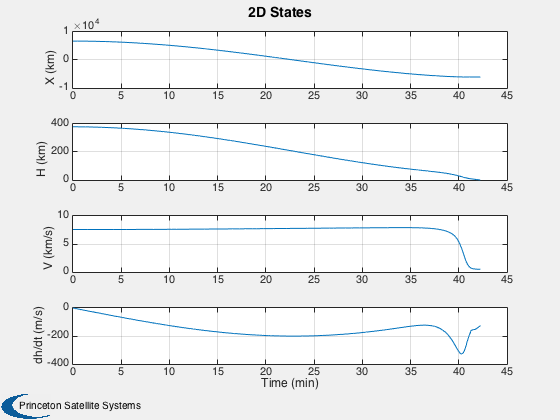
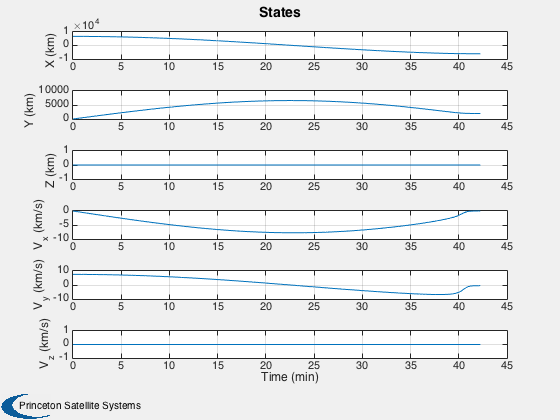
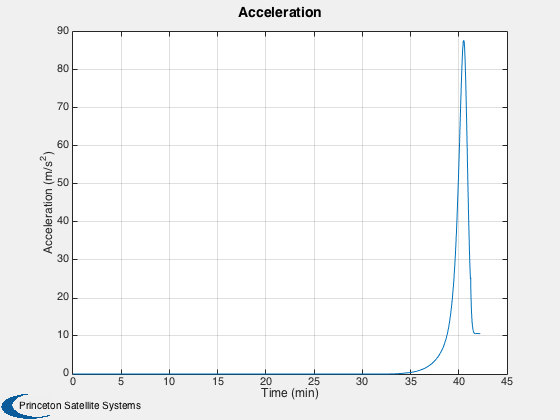
Plot the states

% Create the time array and label
%--------------------------------
[t, tL] = TimeLabl( (0:k)*dT );

yL = {'X (km)' 'H (km)' 'V (km/s)' 'dh/dt (m/s)'};
dhdt = Dot(Unit(x(1:3,:)),x(4:6,:))*1000;

h = Mag(x(1:3,:)) - d.rPlanet;
Plot2D( t, [x(1,:);h;Mag(x(4:6,:));dhdt], tL, yL, '2D States');
yL = {'X (km)' 'Y (km)' 'Z (km)' 'V_x (km/s)' 'V_y (km/s)' 'V_z (km/s)'};
Plot2D( t, x(1:6,:), tL, yL, 'States');

yL = {'Acceleration (m/s^2)'};
Plot2D( t, Mag(f), tL, yL, 'Acceleration');

[t, tL] = TimeLabl( d.time );
yL = {'Heat Flux (W/m^2)'};
Plot2D( t, qDot, tL, yL, 'Heat Flux ' );


%--------------------------------------
% PSS internal file version information
%--------------------------------------

Published with MATLAB® R2014b