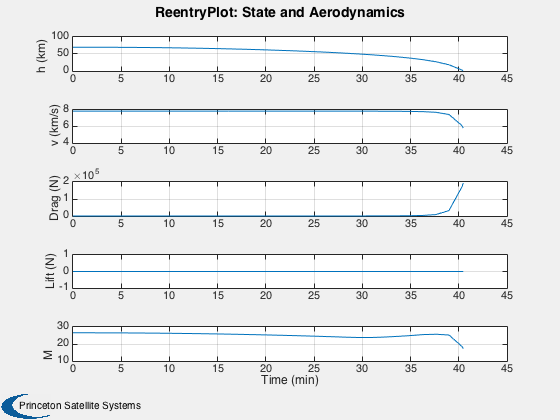
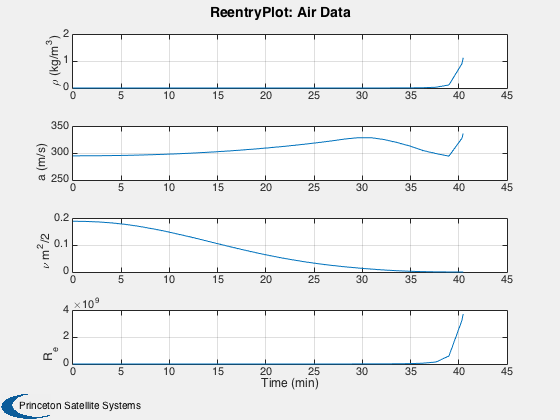
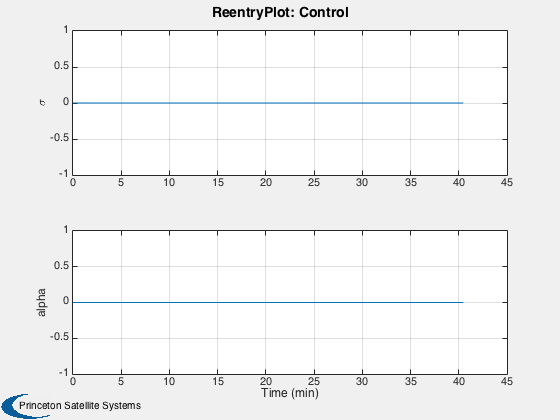
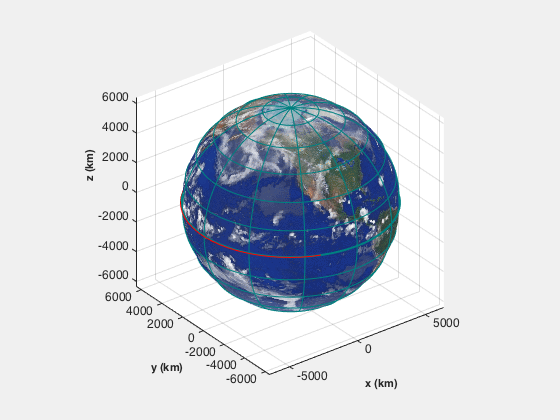
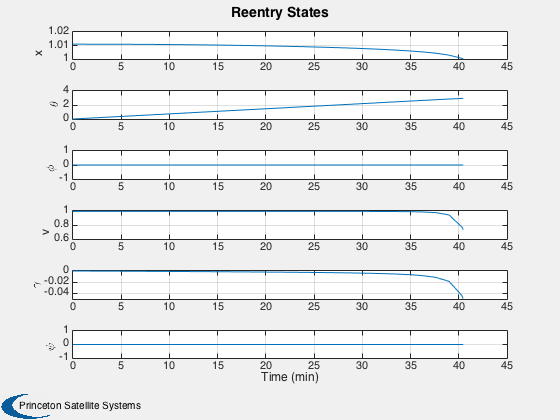
A reentry simulation in spherical coordinates. Uses RHSReentry.m.

------------------------------------------------------------------------
See also Plot2D, TimeLabl, RK4, ReentryPlot, RHSReentry
------------------------------------------------------------------------

Contents

%-------------------------------------------------------------------------------
%    Copyright (c) 2007 Princeton Satellite Systems, Inc.
%    All Rights Reserved.
%-------------------------------------------------------------------------------

Simulation parameters

%----------------------
nSim           = 2400;
dT             = 0.1;
dTLow          = 0.01;

% Constants
%----------
mu             = 3.98600436e14;

Control

%--------
d.alpha        = 0;
d.sigma        = 0;

Parameters

%-----------
d.g            = 9.806;
d.cDP          = 0.001;
d.l            = 10;
d.sRef         = 10;
d.mDry         = 5000; % Dry mass of each stage
d.thrust       = 0; % Thrust of each stage
d.uE           = 405*d.g; % Exhaust velocity of each stage
d.rPlanet      = 6378165;
d.atmData      = load('AtmData.txt');
d.omega        = 2*pi/86400;

Initial states

%---------------
vC             = sqrt(d.rPlanet*d.g);
r              = d.rPlanet + 70000;
v              = sqrt(mu/r)/vC; % Circular orbit
r              = r/d.rPlanet;
x              = [r;0;0;v;0;0;0];

% Plotting arrays
%----------------
x              = [x  zeros(7,nSim)];
u              = zeros(2,nSim+1);
t              = zeros(1,nSim+1);

Simulation

%------------
for k = 1:nSim

  % Propagate one step
  %-------------------
  x(:,k+1) = RK4( 'RHSReentry', x(:,k), dT, 0, d );

  t(k+1)   = t(k) + dT;
  u(:,k+1) = [d.sigma;d.alpha];

  % At low altitude reduce the time step
  %-------------------------------------
  h        = x(1,k+1)*d.rPlanet - d.rPlanet;
  if( h < 10000 )
    dT = dTLow;
  end

  if( h < 1000 ) break; end

end

Plotting

% Shrink the arrays to the parts used
%------------------------------------
nSim = k;
x    = x(:,1:(nSim+1));
u    = u(:,1:(nSim+1));

% Integration is with respect to dimensionaless time
%---------------------------------------------------
t    = t(1,1:(nSim+1))*sqrt(d.rPlanet/d.g);

% Convert the sim variables to dimensional variables and plot
%------------------------------------------------------------
ReentryPlot( x, t, d, u );

% Create the time array and label
%--------------------------------
[t, tL] = TimeLabl( t);
yL = {'x' '\theta' '\phi' 'v' '\gamma' '\psi'};
Plot2D( t, x(1:6,:), tL, yL, 'Reentry States');


%--------------------------------------
% PSS internal file version information
%--------------------------------------

Published with MATLAB® R2014b